Package org.apfloat.internal

package org.apfloat.internal
Default implementations of the apfloat Service Provider Interface (SPI).

The org.apfloat.internal package contains four different implementations of the apfloat SPI, each based on a different primitive element type:

  • LongBuilderFactory, based on element type long: This is the default implementation used by apfloat. It uses the 64-bit long integer as the elementary type for all data storage and manipulation. It usually is faster than the int version on 64-bit JVMs, which is mostly the case today. In some places it uses also double arithmetic, so the processor should be able to perform double-precision floating point operations as well as convert between double and long, for decent performance. For example, on x86-64 and SPARC the 64-bit long version is faster than the 32-bit int version. You can use the long implementation on 32-bit platforms too, however the performance per element is less than half of the int version, even if roughly twice as much data is processed per element. The upside is that this implementation can do much bigger calculations: up to about 3.5 * 1015 digits in radix 10.
  • IntBuilderFactory, based on element type int: It works well for 32-bit platforms that perform integer operations fast (including integer multiplication), and can multiply doubles and convert between double and int with adequate performance. This applies to most workstations today (Intel x86 processors and compatibles, in particular processors with SSE2 support, and most RISC architectures). You can do calculations up to roughly 226 million digits (in radix 10) with this implementation, which should be enough for most purposes.
  • DoubleBuilderFactory, based on element type double: This implementation exists generally only as a curiosity. It will typically perform worse than the long version, and it's only able to do calculations with about 1/20 of its maximum digit length. The only situation where using the double version might make sense is on a platform that performs floating-point arithmetic well, but performs integer arithmetic extremely badly. Finding such a platform today might be difficult, so generally it's advisable to use the long version instead, if you have a 64-bit platform or need the most extreme precision.
  • FloatBuilderFactory, based on element type float: This version is also only a curiosity. The main downside is that it can only perform calculations up to about 1.3 million radix-10 digits. The per-digit performance is also typically less than that of the int version. Unless you have a computer that performs floating-point arithmetic extraordinarily well compared to integer arithmetic, it's always advisable to use the long or int version instead.
For example, the relative performance of the above implementations on some CPUs is as follows (bigger percentage means better performance):
Relative performance of implementations
TypePentium 4Athlon XPAthlon 64 (32-bit)Athlon 64 (64-bit)UltraSPARC II
Int100%100%100%100%100%
Long40%76%59%95%132%
Double45%63%59%94%120%
Float40%43%46%42%82%

(Test was done with apfloat 1.1 using Sun's Java 5.0 server VM calculating π to one million digits with no disk storage.)

Compared to the java.math.BigInteger class with different digit sizes, the apfloat relative performance with the same CPUs is as follows:

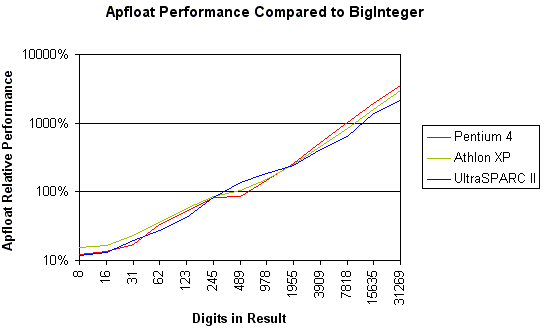
Apfloat and BigInteger comparison

(Test was done with apfloat 1.1 using Sun's Java 5.0 server VM calculating 3n and converting the result to decimal.)

This benchmark suggests that for small numbers – less than roughly 200 decimal digits in size – the BigInteger / BigDecimal classes are probably faster, even by an order of magnitude. Using apfloats is only beneficial for numbers that have at least a couple hundred digits, or of course if some mathematical functions are needed that are not available for BigIntegers or BigDecimals. The results can be easily explained by the smaller overhead that BigIntegers have due to their simpler implementation. When the size of the mantissa grows, the O(n log n) complexity of apfloat's FFT-based multiplication makes apfloat considerably faster than the steady O(n2) implementation of the BigInteger class. For numbers with millions of digits, multiplication using BigIntegers would be simply unfeasible, whereas for apfloat it would not be a problem at all.

All of the above apfloat implementations have the following features (some of the links point to the int version, but all four versions have similar classes):

The apfloat implementation-specific exceptions being thrown by the apfloat library all extend the base class ApfloatInternalException. This exception, or various subclasses can be thrown in different situations, for example:
  • Backing storage failure. For example, if a number is stored on disk, an IOException can be thrown in any of the disk operations, if e.g. a file can't be created, or written to if the disk is full.
  • Operands have different radixes. This is a limitation allowed by the specification.
  • Other internal limitation, e.g. the maximum transform length mathematically possible for the implementation, is exceeded.
Note in particular that numbers, which take a lot of space are stored on disk in temporary files. These files have by default the extension *.ap and they are by default created in the current working directory. When the objects are garbage collected, the temporary files are deleted. However, garbage collection may not work perfectly at all times, and in general there are no guarantees that it will happen at all. So, depending on the program being executed, it may be beneficial to explicitly call System.gc() at some point to ensure that unused temporary files are deleted. However, VM vendors generally warn against doing this too often, since it may seriously degrade performance. So, figuring out how to optimally call it may be difficult. If the file deletion fails for some reason, some temporary files may be left on disk after the program exits. These files can be safely removed after the program has terminated.

Many parts of the program are parallelized i.e. are processed with multiple threads in parallel. Parallelization is done where it has been easy to implement and where it is efficient. E.g. the "six-step" NTT is parallelized, because the data is in matrix form in memory and it's easy and highly efficient to process the rows of the matrix in parallel. Other places where parallelization is implemented are the in-place multiplication of transform results and the carry-CRT operation. However in both of these algorithms the process is parallelized only if the data is in memory - if the data was stored on disk then the irregular disk seeking could make the parallel algorithm highly inefficient.

Many sections of the code are not parallelized, where it's obvious that parallelization would not bring any benefits. Examples of such cases are addition, subtraction and matrix transposition. While parallel algorithms for these operations could certainly be implemented, they would not bring any performance improvement. The bottleneck in these operations is memory or I/O bandwidth and not CPU processing time. The CPU processing in addition and subtraction is highly trivial; in matrix transposition it's outright nonexistent - the algorithm only moves data from one place to another. Even if all the data was stored in memory, the memory bandwidth would be the bottleneck. E.g. in addition, the algorithm only needs a few CPU cycles per element to be processed. However moving the data from main memory to CPU registers and back to main memory needs likely significantly more CPU cycles than the addition operation itself. Parallelization would therefore not improve efficiency at all - the total CPU load might appear to increase but when measured in wall-clock time the execution would not be any faster.

Since the core functionality of the apfloat implementation is based on the original C++ version of apfloat, no significant new algorithms have been added (although the architecture has been otherwise greatly beautified e.g. by separating the different implementations behind a SPI, and applying all kinds of patterns everywhere). Thus, there are no different implementations for e.g. using a floating-point FFT instead of a NTT, as the SPI (org.apfloat.spi) might suggest. However the default implementation does implement all the patterns suggested by the SPI – in fact the SPI was designed for the default implementation.

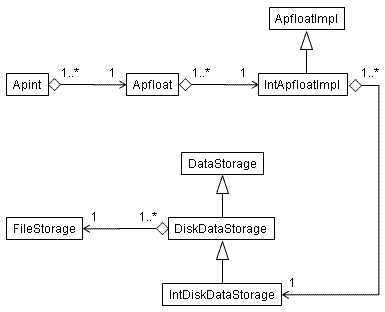
The class diagram for an example apfloat that is stored on disk is shown below. Note that all the aggregate classes can be shared by multiple objects that point to the same instance. For example, multiple Apfloats can point to the same ApfloatImpl, multiple ApfloatImpls can point to the same DataStorage etc. This sharing happens in various situations, e.g. by calling floor(), multiplying by one etc:

Implementation class diagram

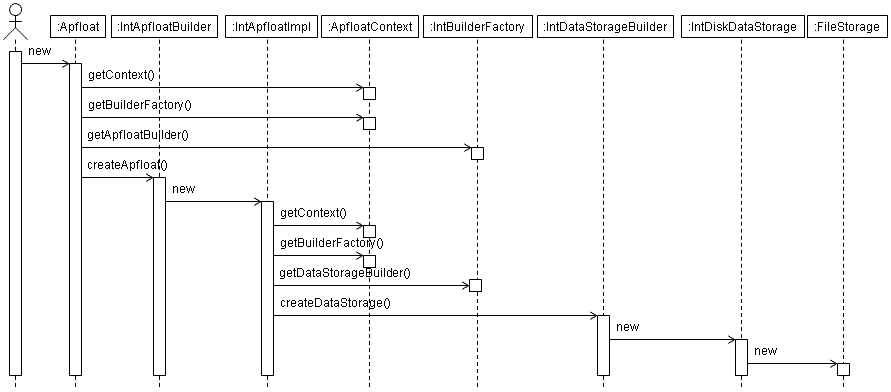
The sequence diagram for creating a new apfloat that is stored on disk is as follows. Note that the FileStorage class is a private inner class of the DiskDataStorage class:

New Apfloat sequence diagram

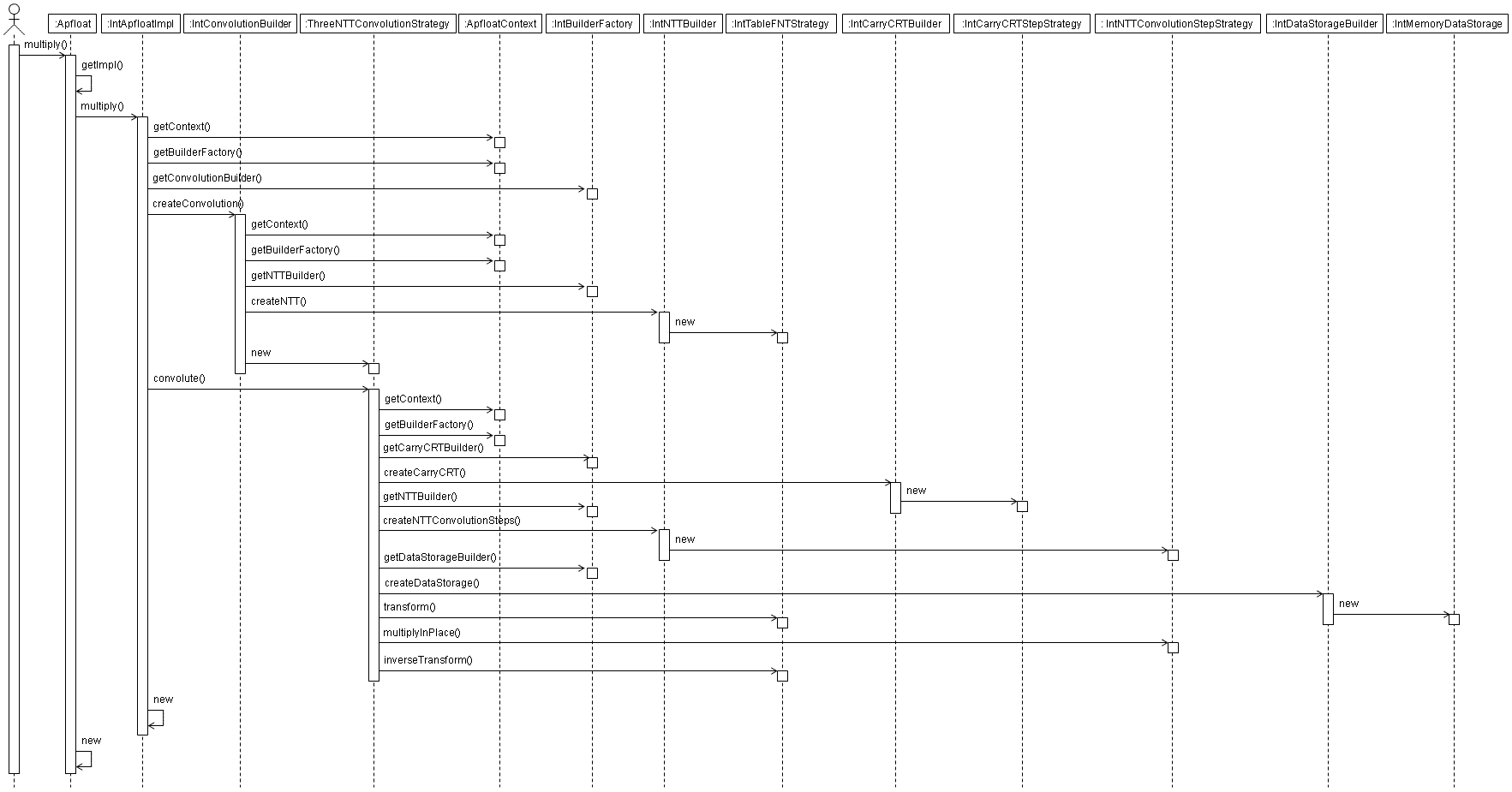
The sequence diagram for multiplying two apfloats is as follows. In this case a NTT based convolution is used, and the resulting apfloat is stored in memory:

Multiplication sequence diagram

Most of the files in the apfloat implementations are generated from templates where a template tag is replaced by int/long/float/double or Int/Long/Float/Double. Also the byte size of the element type is templatized and replaced by 4/8/4/8. The only files that are individually implemented for each element type are: 

BaseMath.java
CRTMath.java
ElementaryModMath.java
ModConstants.java
See Also: